Spatially Distributed Converters
Conventional and Distributed DC/DC Converters
Switched converter ciruits are widely used due to their efficiency. The energe is stored temporarely in inductors and/or capacitors. The next figure shows the network model of a buck converter [5]:
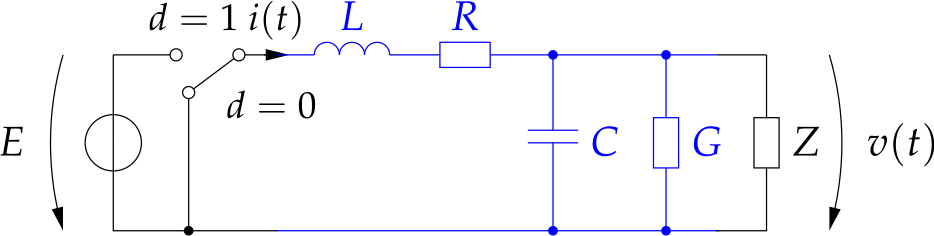
This network can be modeled by ordinary differential equations (ODEs):
\[\begin{array}{rcl} L\tfrac{d i(t)}{d t}+R \,i(t)+v(t)&=&E\, d(t),\\ C\tfrac{d v(t)}{d t}+G \,v(t)+\tfrac{1}{Z}v(t)&=&i(t). \end{array}\]This is a lumped parameter model.
If the power supply and the load are spatially separated, a power line is needed anyway. We could replace the inductor (and possibly the capacity) by a transmission line resulting in the following converter toplogy of a distributed buck converter [5]:
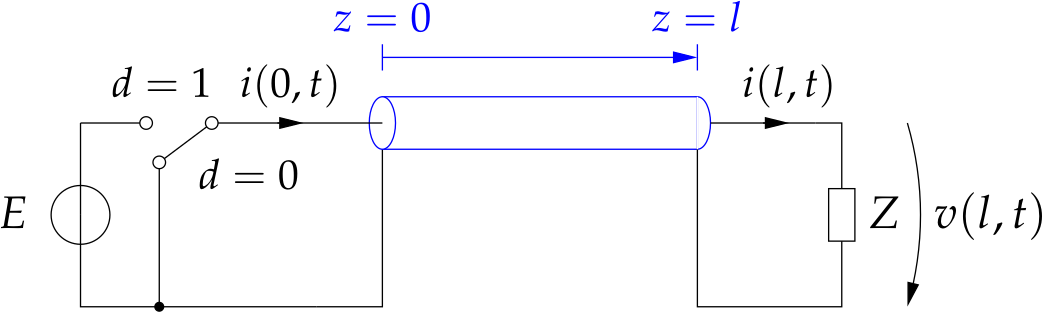
The transmission line can be modeled by the telegrapher’s equation:
\[\begin{array}{rcl} \frac{\partial }{\partial z}v(z,t)+L^{\prime}\frac{\partial }{\partial t}i(z,t)+R^{\prime} i(z,t)&=&0,\\ \frac{\partial }{\partial z}i(z,t)+C^{\prime}\frac{\partial }{\partial t}v(z,t)+G^{\prime} v(z,t)&=&0, \end{array}\]which are partial differential equations (PDEs). With this description we have a distributed parameter model.
Conducted Research on Distributed Converters
In [1] we modeled the buck converter with resistive (i.e., ohmic) load, in [2] with inductive load. In [3,4] we analysed the buck converter under PWM excitation and descriped practical circuit implementations. The feedback control of the distributed buck is investigated in [5,6]. A model of a distributed boost converter is derived in [7].
Github
https://github.com/TUD-RST/current-mode-control-buck-converter
Publications
- Huang, C., Woittennek, F., Röbenack, K. (2013, September). Steady-state analysis of a distributed model of the buck converter.
In 2013 European Conference on Circuit Theory and Design (ECCTD) (pp. 1-4). IEEE. - Huang, C., Woittennek, F., Röbenack, K. (2015). Distributed parameter model of the buck converter with constant inductive load.
IFAC-PapersOnLine, 48(1), 691-692. - Röbenack, K., Herrmann, R. (2022, October). Analysis, simulation and implementation of a distributed buck converter.
In 2022 26th International Conference on System Theory, Control and Computing (ICSTCC) (pp. 213-218). IEEE. - Röbenack, K., & Herrmann, R. (2023). Distributed buck converter realization based on a transmission line.
SYSTEM THEORY, CONTROL AND COMPUTING JOURNAL, 3(1), 29-35. - Röbenack, K., & Palis, S. (2023). Set-point control of a spatially distributed buck converter.
Algorithms, 16(1), 55. - Röbenack, K.; Gerbet, D. Current-Mode Control of a Distributed Buck Converter with a Lossy Transmission Line.
Electronics 2024, 13(17), 3565. - Röbenack, K., & Bärnklau, H. (2023, October). A Spatially Distributed Boost Converter–Modeling and Simulation.
In 2023 27th International Conference on System Theory, Control and Computing (ICSTCC) (pp. 480-486). IEEE.